图基础概念

---

图

在图数据库及图计算的概念中，图（Graph）指的是由若干给定的点及连接两点的线所构成的图形（如左图），而非常规概念中图像（如右图）的图（Image）。

这种图形通常用来描述事物之间的某种特定关系，同时也是数学分支中图论（Graph Theory）的主要研究对象。

图的定义可描述为：

图（Graph）是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V，E)，其中，G 表示一个图，V 是图 G 中顶点的集合，E 是图 G 中边的集合。

---

点

又称顶点（Vertex），是组成图的最小元素之一，一个图可以包含多个顶点，例如下图是一个包含5个点的图。

在实际应用中，顶点常用于描述一个事物实体，在不同场景下有不同含义，可以代表一个人，也可以代表一家公司，还可能是一种抽象的思想，或是一次行为。

---

边

作为连接两个顶点的线，边常用于描述事物实体之间的关系，边可以有方向，也可以无方向，一个图中可以包含多条边，两个点之间也可以包含多条边，例如下图是一个包含6条边的图。

以有向边构成的图，被称为有向图。在有向图中，从A点出发到达其他顶点的边称为A点的出边，从其他顶点指向A点的边称为A点的入边，出边与入边的总数分别称为A点的出度与入度。

在实际应用中，边常用与描述两个事物实体之间的某种关联，在不同场景下有不同含义，可以代表从属关系，也可以代表一次转账行为。

---

属性

随着市场应用对业务灵活性的需求日益提升，在一个实际场景中所需要存储的数据，除了数据量上的提升之外，对于异构数据、集成新数据和分析等方面都需要更强的灵活性，图数据结构可以很好的满足这一点。

如今，最主要的图数据结构模型有两种：

• 属性图（Property Graph）
• RDF图（Resource Description Framework Graph）

下面主要以属性图为例进行介绍。

与传统关系型数据库的构建策略不同，属性图将构成数据之间拓扑关系的点数据与边数据，直接作为图数据的基本数据实体进行存取，其他用于辅助描述顶点、边的数据，可以作为属性数据存储。

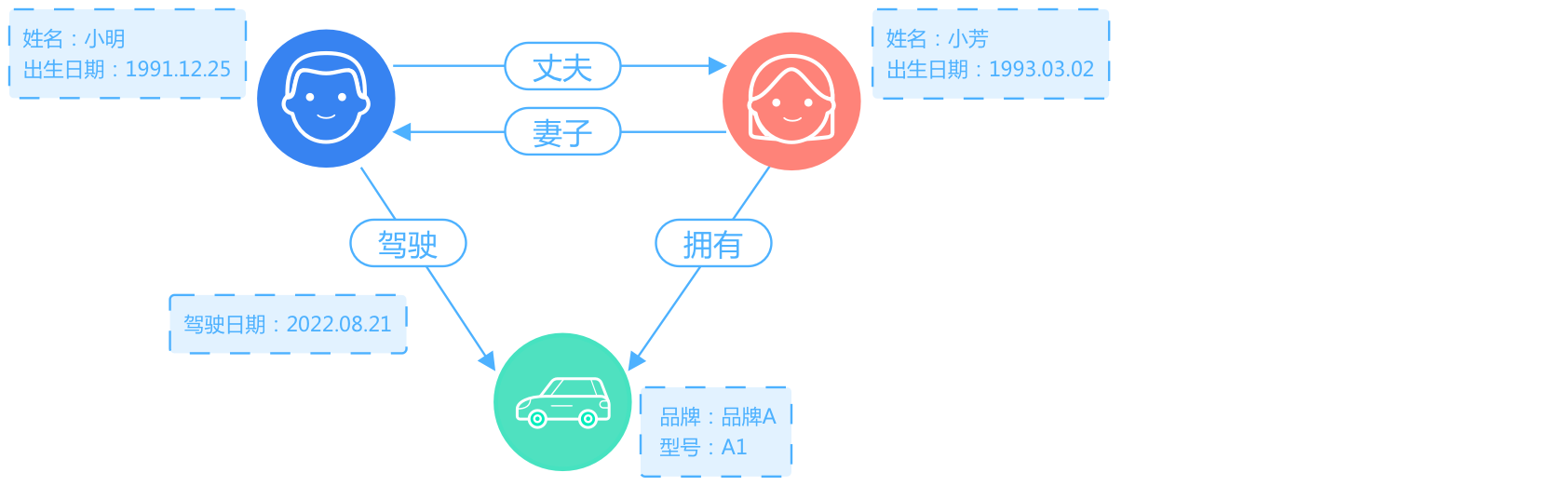
• 实体

图中顶点代表实际场景中的实体或抽象概念，例如：人、用户、公司、账号、产品、地址、电话号码、设备、类型、状态、角色等。

• 关系

图中边代表实体与实体之间的关系，例如：（某人和某人）是同事关系、（员工）受雇于（公司）、（公司）受（另一公司）控股、（顾客）购买（产品）等。

• 属性

属性用来补充描述实体和关系。例如上图的实体人物，拥有姓名、出生日期等属性。

---

邻居

在有向图中，如果存在一条从v₁指向v₂的边，则称v₂为v₁的一个邻居节点，简称邻居。

在无向图中，如果v₁是v₂的邻居，则v₂也是v₁的邻居。

邻居的定义可描述为：

在一个图G(V，E)中，点vj的邻居集合 = { v_j ∈ V ｜ v_iv_j ∈ E}

实际上，一个点通过某路径能够到达的所有点集即为这个点的邻居。

可以经过1条边到达的点被称作1阶（跳）邻居，经过2条边能够到达的点被称作2阶（跳）邻居，以此类推。

下图中，对于v₁和v₂来说，二者互为1跳邻居。

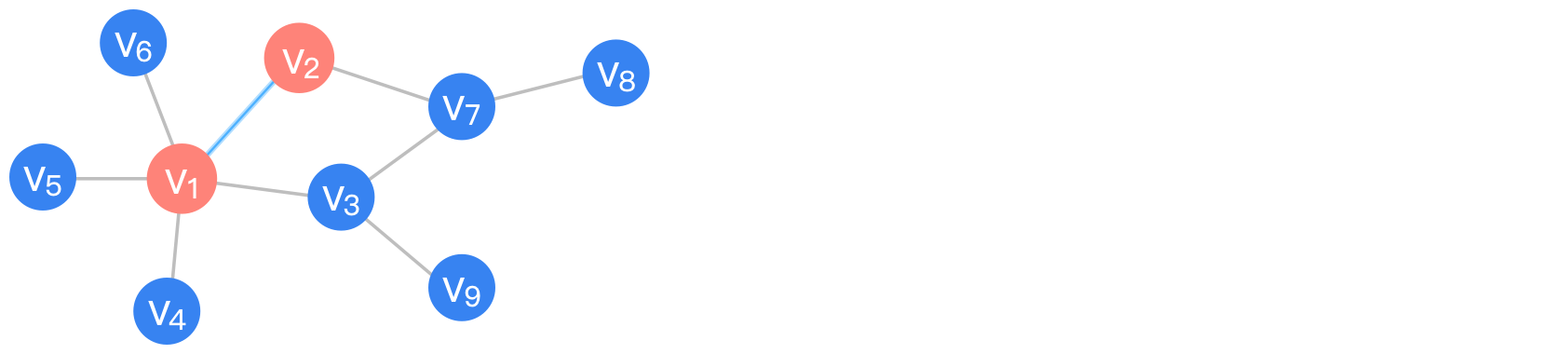
v₁和v₇之间，需要经过2条边才能相互到达，它们是彼此的2跳邻居。

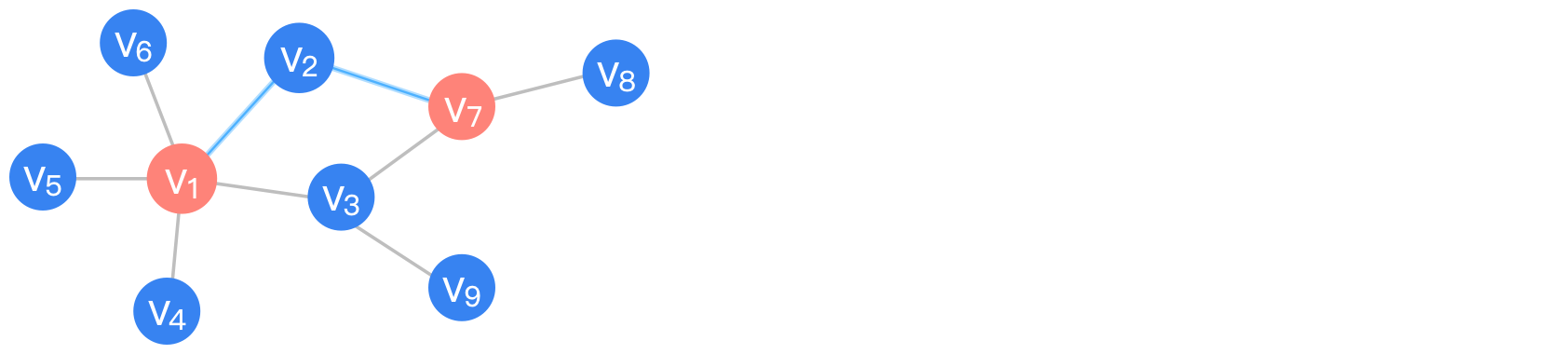
同理，v₁和v₈是彼此的3跳邻居。

---

路径

在一个图中，由一个有限或无限的边序列组成的结构数据，称为一条路径，这些边连接着一系列的点。

在大多数场景的描述中，统称一个由点、边组成的交错序列，为一条路径（Path）。

部分高级API及需要精确定义各种不同路径的场景下，会采用图论中的基本术语进行进一步的区分：

• 途径（Walk）

一个点、边的交错序列，称为一条途径

• 迹（Trail）

对于一条途径w，每条边各不相同，则称该w为一条迹

• 路径（Path）

对于一条迹w，除起点和终点外，每个点各不相同，则称w为一条路径，又称简单路径（Simple path）

• 回路（Circuit）

对于一条迹w，起点与终点相同，则称w为一条回路

• 环/圈（Cycle）

对于一条简单路径w，起点与终点相同，则称w为一条环路，简称环，仅由一条线组成的环，称为自环

• 轨道（Track）

部分概念中，对于一条途径w，每个点各不相同，则称w为一条轨道

在某些金融场景下，基于图数据进行环路检测，可以提供独特的分析能力。例如：在客户的转账关系网络中，利用环路检测，搜索资金环路，挖掘到潜在的洗钱团伙的资金链路，以及链路中的详细流水情况，为后续业务排查提供更多参考。

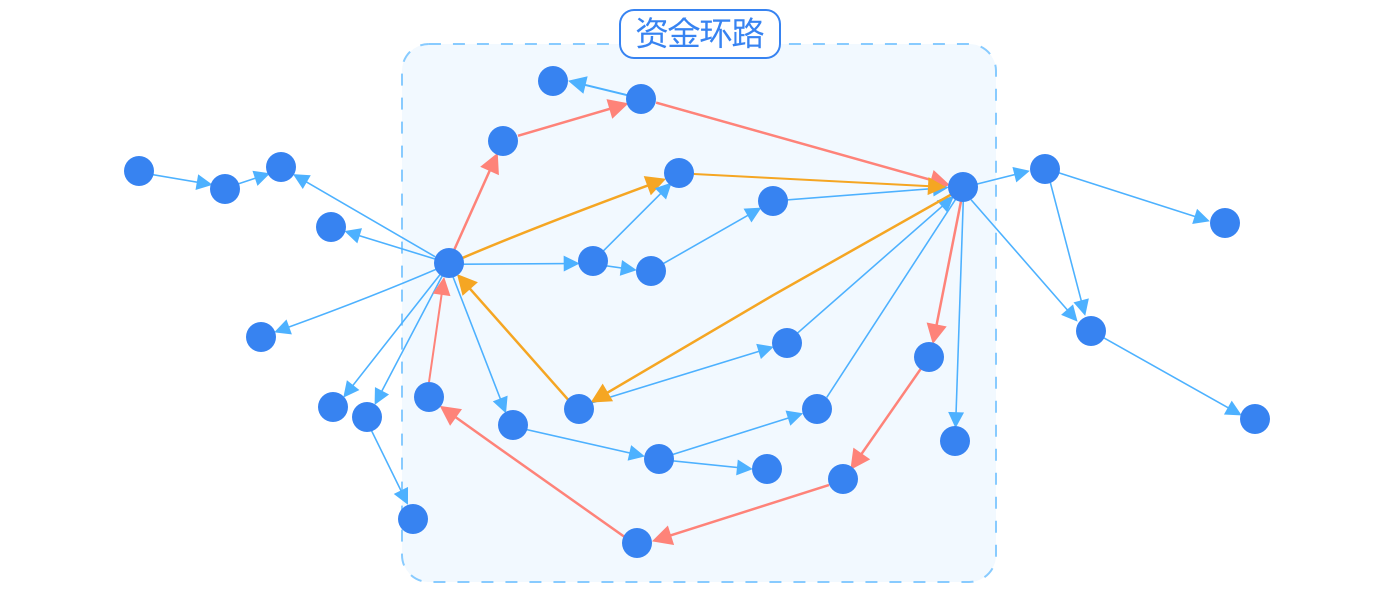
中小企业常常通过企业担保来获得贷款，而随着担保链条的不断延长，会形成担保环路，在客户的担保关系网络中，利用环路探测，搜索客户担保环路，分析担保环路中的企业相互关系，为对公贷款业务风控提供参考。

---

子图

图数据的查询结果，常以子图结构返回结果，同时也是图论中的基本概念之一，指节点集和边集分别是另一个图节点集的子集和边集的子集的图，每一个图同时也是自身的子图。

子图的定义可描述为：

对于一个图G(V，E)，如果存在另一张图H(V', E')，满足V'⊆V且E'⊆E，则称H是G的子图（Subgraph），记作H⊆G